|
王明贵
(中国建筑科学研究院,北京100013)
[提 要] 应用地基与基础相互作用原理,研究了建筑结构中筏板基础的计算方法,在计算中考虑了上部结构刚度的影响和土的塑性问题,为工程应用研制了筏板基础计算程序TBSA-F  ,已被应用于高层建筑结构的地基基础工程设计中。 ,已被应用于高层建筑结构的地基基础工程设计中。
[关键词] 筏板基础,相互作用,上部结构刚度
高层建筑对基础作用的荷载较大,为满足地基土的承载力要求,必须将基础整片连续地设置于建筑物之下,如筏板基础等,从而大大地减少了对地基土的附加压力。在大多数情况下,这种连续性基础不仅能满足地基土的承载力要求,而且还依靠基础的连续性和双向抗弯性能来加强建筑物的整体刚度,以利于调整不均匀沉降,并且还能改善建筑物的抗震性能。
依据温克尔(Winkler,1867)假定,地基土受压被看作是许多彼此不相联接的弹簧体系的受压,可见它是阿基米德定律的直接推广。实践表明,这对浅地基或受条形荷载的构件(如弹性地基梁)分析是比较符合的。随着计算机技术的发展,考虑地基土为连续介质模型的分析成为可能。
一、 地基模型
在建筑物荷载作用下,地基与基础紧密接触。假定基础是弹性的,地基土是层状结构的,并具有弹塑性性能。地基与基础之间相互作用受力分析应满足整体平衡和变形连续性条件。 如图1所示弹性半空间体的计算简图,布辛涅斯克解答为 如图1所示弹性半空间体的计算简图,布辛涅斯克解答为
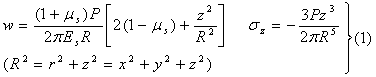

*中国建筑科学研究院基金项目
式中, 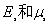 是地基土的弹性常数。在水平边界上任意一点的法向位移即沉降为 是地基土的弹性常数。在水平边界上任意一点的法向位移即沉降为
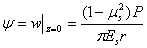 (2) (2)
可见,沉降变形是光滑连续地发展在力作用点之外,但衰减很快。如果是受连续分布的法向力p(x、y)作用,则用积分表达为
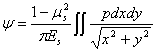 (3) (3)
地基土是层状结构的,如果任意第k层土的弹性常数为 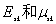 ,为简化计算,假定土在完全侧限条件下的压缩应变 ,为简化计算,假定土在完全侧限条件下的压缩应变 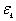 与附加应力 与附加应力 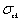 成正比,即 成正比,即
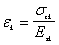 (4) (4)
则沉降变形
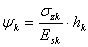 (5) (5)
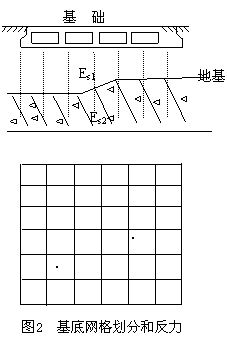
式中, 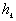 为第k层土的厚度。为便于计算机应用计算,将地基表面划分一些有限元计算网格来描述任一点i的沉降与j点作用力之间的关系。设网格总数为L,各网格的面积分别为ai( i=1,2,…,L),相应的压力分别为pi( i=1,2,…,L),每一个网格上的压力可认为是均布的。如图2所示。按叠加原理,第i网格之中点的沉降 为第k层土的厚度。为便于计算机应用计算,将地基表面划分一些有限元计算网格来描述任一点i的沉降与j点作用力之间的关系。设网格总数为L,各网格的面积分别为ai( i=1,2,…,L),相应的压力分别为pi( i=1,2,…,L),每一个网格上的压力可认为是均布的。如图2所示。按叠加原理,第i网格之中点的沉降  为所有各网格上压力分别引起的沉降总和,即 为所有各网格上压力分别引起的沉降总和,即
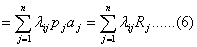 
或写成矩阵形式为
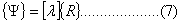
式中, 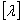 为地基柔度矩阵, 为地基柔度矩阵,
其柔度系数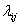 为第j点单位 为第j点单位
力引起第i点的沉降。在(4)
式的假定下,各土层的沉降
叠加得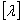 的元素为 的元素为
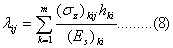
式中,  为地基附加压应力, 为地基附加压应力,
在这里由(1)式取P=1即可。
m是地基土计算总层数。
二. 弹性地基板
根据板弯曲理论的势能泛函 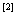
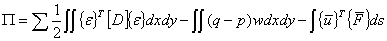 (9) (9)
式中,
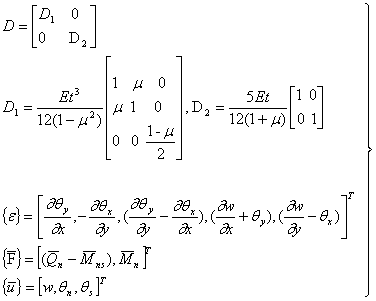 (10) (10)
其,t为板厚,E和 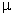 为板的弹性常数,q为板面上作用的分布荷载,p为板底土的分布力,w和 为板的弹性常数,q为板面上作用的分布荷载,p为板底土的分布力,w和 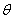 分别为板的挠度和转角,n和s分别为板边界的法向和切向座标。将板划分为有限元计算网格后(与地基土的网格一致),第i结点的挠度w和转角 分别为板的挠度和转角,n和s分别为板边界的法向和切向座标。将板划分为有限元计算网格后(与地基土的网格一致),第i结点的挠度w和转角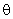 记为 记为
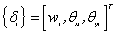 (11) (11)
设单元网格内的位移
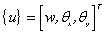 (12) (12)
为该单元各结点位移
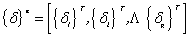 (g为单元结点数) (13) (g为单元结点数) (13)
的插值函数,即
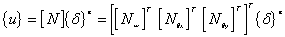 (14) (14)
则
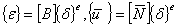 (15) (15)
其中 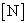 为形函数 为形函数 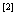 。则式中 。则式中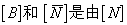 运算得到的矩阵。根据最小势能原理 运算得到的矩阵。根据最小势能原理
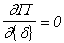 (16) (16)
将(9)代入(16),得
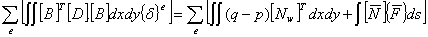 (17) (17)
令
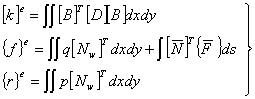 (18) (18)
则(17)式改写成
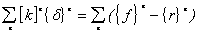 (19) (19)
即
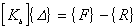 (20) (20)
在式(20)中,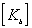 为板单元的总刚度矩阵, 为板单元的总刚度矩阵, 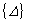 为结点位移列阵, 为结点位移列阵, 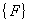 为结点荷载列阵, 为结点荷载列阵, 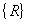
为结点反力列阵。根据式(7),得
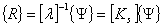 (21) (21)
式中为地基单元的总刚度矩阵。 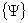 为沉降变形,它与板的挠度相等, 为沉降变形,它与板的挠度相等, 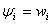 ,即连续性条件。则方程(20)为 ,即连续性条件。则方程(20)为
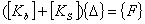 (22) (22)
方程(22)就是地基与基础板相互作用的控制方程,便于计算机应用计算。
最后,记板中的内力为
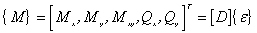 (23) (23)
则有
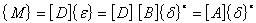 (24) (24)
式中 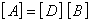 为板的内力矩阵。 为板的内力矩阵。
三. 相关问题
为了将上述的地基与基础相互作用一般原理应用到工程实际中去,还需处理几个相关问题,本文从工程实用计算上近似考虑了以下这些问题。
3.1 土的塑性影响
根据土力学原理,土的临塑压力为[3]
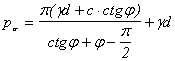 (25) (25)
式中d为基础的埋置深度, 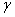 为地基土的密度,c为地基土的粘聚力, 为地基土的密度,c为地基土的粘聚力, 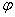 为地基土的内摩擦角。当地基土所承受的压力超过了pcr后,土体就会发生局部剪力破坏,基底反力重分布。随着压力的增加,土的塑性区逐渐扩展。但经验证明,只要塑性区的范围不超过某一限度,就不致影响建筑的安全使用,这时的控制条件应是沉降量。因此,有经验表明,在中心荷载作用下,塑性区的最大深度可以控制在基础宽度的四分之一,相应的荷载用 为地基土的内摩擦角。当地基土所承受的压力超过了pcr后,土体就会发生局部剪力破坏,基底反力重分布。随着压力的增加,土的塑性区逐渐扩展。但经验证明,只要塑性区的范围不超过某一限度,就不致影响建筑的安全使用,这时的控制条件应是沉降量。因此,有经验表明,在中心荷载作用下,塑性区的最大深度可以控制在基础宽度的四分之一,相应的荷载用 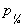 表示,即 表示,即
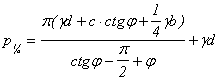 (26) (26)
在地基与基础之间的互相作用计算中,为了考虑土的塑性,要用迭代法求解方程(20)和(21),并引入土的临塑压力,使每次迭代的反力不超过土的临塑压力pcr或 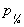 ,即 ,即 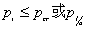 。考虑了土的塑性后,基底反力趋近平缓,板中内力有所减少。从而可节省配筋量。但应用临塑公式(25)或(26)时应注意,该公式是在均布条形荷载的浅基础情况下导出的,应作深宽修正,可参考地基承载力的修正方法 。考虑了土的塑性后,基底反力趋近平缓,板中内力有所减少。从而可节省配筋量。但应用临塑公式(25)或(26)时应注意,该公式是在均布条形荷载的浅基础情况下导出的,应作深宽修正,可参考地基承载力的修正方法 。 。
3.2 上部结构刚度的影响
上部结构刚度对地基不均匀沉降和基础挠曲有约束作用,约束的强弱与上部结构的型式有关,较为精确地分析是很困难的,但考虑这种约束影响与否对基础内力计算有一定的影响。我国有关规范采用了G.G迈耶霍夫(Meyerhof,1963)提出的“等代刚度梁法”来粗略估计上部框架结构刚度对基础弯曲的影响[3],即
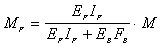 (27) (27)
但对于二维的基础问题,整体弯矩M的概念就不适当了。另外,当上部框架层数较大时,该方法对上部结构整体刚度的估计偏高。实测基础中钢筋应力表明,钢筋应力并不随荷载层数的增加而一直增加,上部在逐层施工的过程中,对基础是逐层加载的,而层刚度滞后逐层形成,在施工初始阶段,层荷载增加,但层刚度还未形成,基础随荷载增加而内力增大,当施工到一定层数时,层刚度渐渐形成,这时虽然施工层荷载增加,但基础内力增大趋缓,形成了对基础自由弯曲的制约作用,这种制约作用是通过基础平面上的墙柱构件抗
弯来实现的。因此,可计算出各墙肢和柱的线刚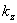 和转动刚度 和转动刚度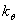 ,如第i结点上的柱子刚度k ,如第i结点上的柱子刚度k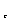 记为 记为
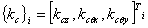 , i=1,2,3,…, , i=1,2,3,…, 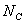 (28) (28)
其中,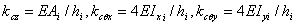 ,(h为层高)。将柱的刚度分配到附近的单元结点上,所有柱子形成一个总刚度矩阵 ,(h为层高)。将柱的刚度分配到附近的单元结点上,所有柱子形成一个总刚度矩阵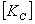 作为筏板弯曲的附加刚度,离散地作用在筏板中过墙柱处的结点上,从而能体现出柱距(跨度)不同的影响。 作为筏板弯曲的附加刚度,离散地作用在筏板中过墙柱处的结点上,从而能体现出柱距(跨度)不同的影响。
筏板基础和上部结构相互作用计算也容易实现:
第一步,计算上部结构,取筏板基础为嵌固端;
第二步,用上部结构计算的底层柱脚力作为筏板基础计算的荷载来计算筏板的内力和位移(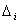 , ,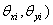 ; ;
第三步,由第二步可得各柱的伸缩变形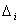 及其最小的 及其最小的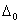 ,从而可计算出各柱的次生力系: ,从而可计算出各柱的次生力系:
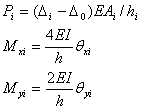 (29) (29)
第四步,用第三步的这些力去修改第一步的荷载{P};
第五步,重复一至四步,直到前后两次计算结果相近为止(收敛精度控制)。
这些计算过程必须由计算机完成。
3.3 桩基础刚度的引入
若是桩筏基础,要引入桩的刚度,其定义为桩顶产生单位变位(沉降或转动)所需的力,其值由现场压桩实验所得,也可按公式计算。记为
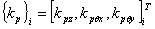 , i=1,2,,3,…, , i=1,2,,3,…, 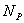
工程桩一般较大,作用面宽,需将桩的刚度分配到附近的单元结点上,所有桩形成一个总刚度矩阵 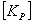 作为基础的附加刚度,离散地分布在地基刚度矩阵中桩位所在处的各单元结点上。但是,桩基刚度矩阵与地基刚度矩阵不能简单叠加,否则,桩的反力计算结果会因单元网格划分的大小不同而有很大差别的奇怪现象产生。 作为基础的附加刚度,离散地分布在地基刚度矩阵中桩位所在处的各单元结点上。但是,桩基刚度矩阵与地基刚度矩阵不能简单叠加,否则,桩的反力计算结果会因单元网格划分的大小不同而有很大差别的奇怪现象产生。
四. 计算程序实现
按上述地基与基础相互作用原理,结合我国现行规范,我们研制开发了基础计算程序TBSA-F[4],已通过专家鉴定,并应用于工程实际中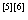 。该计算程序能自动划分有限元网格和自动处理相关的问题(设有选择开关),可操做性强,无论用户对有限元理论了解的程度如何,都能方便地使用该程序。有限元计算数据很多,限于篇幅,我们将在另文讨论工程计算数据分析。 。该计算程序能自动划分有限元网格和自动处理相关的问题(设有选择开关),可操做性强,无论用户对有限元理论了解的程度如何,都能方便地使用该程序。有限元计算数据很多,限于篇幅,我们将在另文讨论工程计算数据分析。
参 考 文 献
1 徐芝纶编。弹性力学。人民教育出版社,1979。
2 浙江大学。弹性和塑性力学中的有限单元法。机械工业出版社,1981.8。
3 华南理工大学等编。地基及基础。中国建筑工业出版社,1991.11。
4 王明贵。建筑结构基础计算程序TBSA-F的研究。建筑科学报告,1997.5
5 陈四川。北京首都时代广场筏基设计与施工。第十五届全国高层建筑结构学术交流会论文集。1998
6 王明贵等。高层建筑中主楼与裙房基础协同工作计算研究。第十五届全国高层建筑结构学术交流会论文集。1998
Calculating Analysis and Engineering Application on the Mat Foundation
Wang Ming Gui,
(China Academy of Building Research,Beijing)
Abstract
This manuscript has done research on the computational methods of the mat foundation with the interactive principles of soil and base. The effects on the superstructures rigidity and the plastics of the soil have been considered in the calculating methods. The computational programs have been made and applied in the mat foundation engineering of tall buildings by means of these calculating methods .
Key words: mat foundation, interaction , superstructure rigidity
|