钢异形柱弯扭相关屈曲研究
王明贵 张莉若 谭世友
(中国建筑科学研究院 北京 100013)
摘要 本文用弹性薄壁柱理论,推导了开口任意截面柱弯扭屈曲相关方程,并由此简化到单轴对称截面、双轴对称截面经典方程。进而研究了L形柱轴向受压的承载力即φ-λ曲线,以便工程设计应用。
关键词 钢异形柱,弹性薄壁柱理论,相关屈曲
Research on the Torsional-Flexural Interactive Buckling
of Steel Abnormity-section Columns
Wang Ming-gui zhang li ruo Tan shi you
(China Academy of Building Research, Beijing 100013)
[Abstract] This paper has derived the general equations of torsional-flexural interactive buckling for abnormity thin-walled open sections columns by means of the theory of elastic thin-walled column. Then the general equations have been simplified to the classical buckling equations of the columns with a or doubly symmetrical sections. The bearing capacity i.e. φ-λ graph has been studied for a thin-walled column of L-section subjected to longitudinal compress so as to be applied in engineering.
[Keywords] steel abnormity-section columns; theory of elastic thin-walled column; interactive buckling
1、前言
在钢结构住宅设计中,结构体系主要是用热轧H型钢建造多层(4~6层)或小高层(7~18层)的框架结构,H型钢柱截面尺寸一般在200mm×200mm至400mm×400mm,再加上保护层和饰面,柱子在室内凸出,影响建筑美观,使用不方便。其实,钢筋混凝土框架结构也存在类似的问题,但钢筋混凝土结构为此研究了一种异形柱(肢长和肢宽比为2~4,区别于短肢剪力墙─肢长和肢宽比为5~8),应用于住宅建筑中,较好地解决了室内柱角凸出的问题。由此设想,在钢结构住宅建筑中若能使用钢异形柱,就能解决钢结构住宅建筑室内柱角凸出问题。例如中柱用十字形截面、边柱用T形截面、角柱用L型截面,它们都由H型钢和T型钢组合而成,我们称它们为钢异形柱,如图1所示。我国现行《钢结构设计规范》第5.2条对十字形柱和T形柱给出了设计计算公式,但没有图1(c)所示L形柱的设计计算方法,有关资料查阅也未见这方面的研究报导文献。因此,本文将研究L形钢异形柱承载力,为钢结构住宅应用做理论研究。
本文用弹性薄壁柱理论,推导了任意开口截面柱弯扭屈曲相关方程,并由此简化到单轴对称截面、双轴
轴对称截面的柱压弯屈曲经典方程。进而研究了L形截面柱轴向受压的承载力及其φ-λ曲线,以便工程设计应用。
2、任意开口截面柱弯扭屈曲相关方程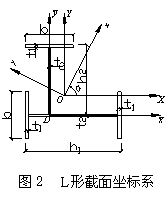
如图2所示的L形截面,没有对称轴,属于任意开口薄壁截面,其柱在弯曲变形的同时会产生扭转。翼缘厚度为t1,腹板厚度为t2,截面宽为h1,高为h2。我们用薄壁柱理论研究这种任意开口截面柱弯扭屈曲的假定是:弹性小变形、中面的剪应变为零、各横截面的周线不变形即刚性周边。在图2坐标系中,取z轴为柱纵向,定义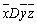 为工程坐标系, 为工程坐标系,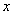 O O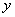 z为形心主坐标系,o为形心。在结构整体计算中,我们首先得到的是柱的工程坐标系内力 z为形心主坐标系,o为形心。在结构整体计算中,我们首先得到的是柱的工程坐标系内力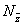 、 、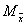 、 、 、 、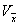 、 、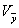 ,则在形心主坐标系中,它们被变换为: ,则在形心主坐标系中,它们被变换为:
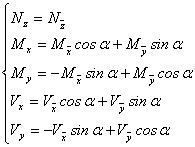 (1) (1)
式中 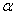 为工程坐标轴与形心主轴的夹角。同理,也可得到截面的几何量变换公式。 为工程坐标轴与形心主轴的夹角。同理,也可得到截面的几何量变换公式。
根据薄壁柱理论结果,对于同时受有拉或压(P)、弯曲(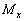 、 、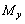 )、扭转( )、扭转(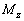 )和剪力 )和剪力 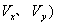 作用的开口薄壁杆件,截面正应力、剪应力可分别写为: 作用的开口薄壁杆件,截面正应力、剪应力可分别写为:
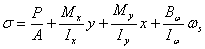 (2) (2)
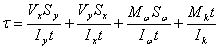 (3) (3)
适中ω是扇形坐标。而带ω下标的是与扇形坐标有关的量[1],限于篇幅从略。若令z截面剪心S的位移为u和
v,绕剪心的扭转角为φ,总事能为: 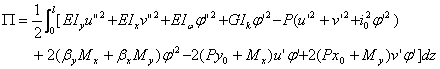
(4)
式中 E为材料弹性模量;l为构件长度;
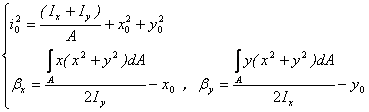 (5) (5)
为不对称截面常数。 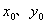 为剪心坐标。则根据势能驻值原理,由 为剪心坐标。则根据势能驻值原理,由 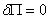 ,可得三个平衡方程: ,可得三个平衡方程: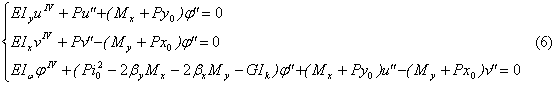
如不计屈曲前变形,代入适合边界条件(如简支)的变形函数,并令:
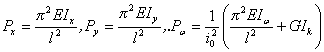 (7) (7)
可得: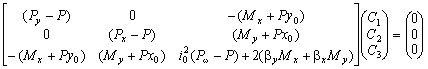 (8) (8)
将上式写为: 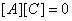 ,由 ,由 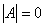 ,即可得任意截面柱弯扭屈曲相关方程: ,即可得任意截面柱弯扭屈曲相关方程:
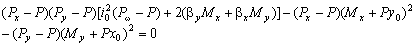 (9) (9)
或 (10) (10)
式中 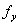 为材料屈服强度, 为材料屈服强度, 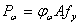 , ,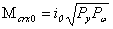 , ,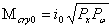 , ,
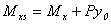 , , 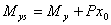 (11) (11)
3、任意截面柱轴心受压
对于双向偏心受压杆件,偏心距ex和ey都是以主轴的正方向为正,负方向为负,,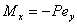 , ,
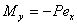 ,式(9)可写为: ,式(9)可写为:
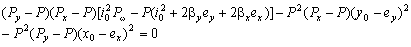 (12) (12)
利用迭代法或数学计算工具Mathematica 5.0可得到不考虑屈曲前变形的任意截面压弯构件的弹性弯扭屈曲荷
载。
对任意截面柱轴心受压,有ex=ey=0,则(12)式成为
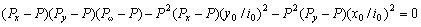 (13) (13)
1) 当单轴对称截面轴心受压时,设对称轴为y,则 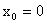 ,剪心距为 ,剪心距为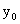 , ,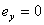 ,式(13)可改写为: ,式(13)可改写为:
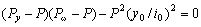 (14) (14)
解方程(14),得单轴对称截面发生弹性弯扭屈曲时绕截面对称轴y的屈曲荷载为
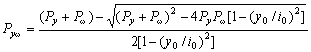 (15) (15)
令 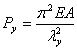 , ,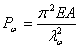 , ,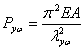 ,代入上式可得[2]: ,代入上式可得[2]:
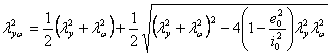 (16) (16)
式中 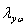 为弯扭屈曲换算长细比,而 为弯扭屈曲换算长细比,而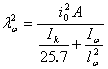 (17) (17)
2) 当双轴对称截面轴心受压时,有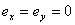 ,式(13)可改写为: ,式(13)可改写为:
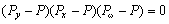 (18) (18)
则 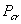 应为 应为 中最小值,即 中最小值,即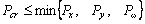 ,构件将发生绕x(或y轴)的弯曲屈曲或者绕纵轴的扭转屈曲。 ,构件将发生绕x(或y轴)的弯曲屈曲或者绕纵轴的扭转屈曲。
任意截面柱轴心受压临界屈曲荷载由方程(13)解三次方程即得,对于本文图2所示的L形截面柱,由方程
(13)的解和ANSYS有限元计算结果被列入表1中以便比较(注:L形截面尺寸为h1=250㎜,h2=187.5㎜,b=
125㎜, t1=9㎜, t2= 6㎜。两端简支,钢材采用Q345,构件强度极限为:
A*fy=5820mm2*345MPa=2007.9kN),同时给出曲线图3所示。计算还表明:相同的用钢量和柱长,L形钢
柱的承载力要比常规H型钢柱高。
若引入轴心受压柱稳定系数 ,定义 ,定义
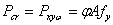 和 和 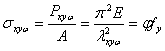 (19) (19)
则有 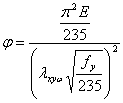 (20) (20)
表1 L形钢柱轴心受压屈曲特征值数值分析
|
编 号 |
柱 长 |
本文(13)式 |
ANSYS 特征值 |
|
1 |
3.0m |
1785.15kN |
1769.35kN |
|
2 |
3.3m |
1562.68kN |
1550.75kN |
|
3 |
3.6m |
1389.47kN |
1383.73kN |
|
4 |
3.9m |
1257.34kN |
1253.10kN |
|
5 |
4.2m |
1152.04kN |
1148.85kN |
|
6 |
4.5m |
1066.61kN |
1064.18kN |
|
7 |
4.8m |
996.20kN |
994.34kN |
|
8 |
5.1m |
937.34kN |
935.91kN |
|
9 |
5.4m |
887.50kN |
886.39kN |
|
10 |
5.7m |
844.79kN |
843.92kN |
|
11 |
6.0m |
807.78kN |
807.09kN |
|
|
|
|
令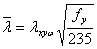 ,用表1数据,可得 ,用表1数据,可得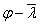 曲线,并与《钢结构设计规范》中b、c类曲线进行比较, 曲线,并与《钢结构设计规范》中b、c类曲线进行比较,
如图4所示。本文中的 为理想线弹性条件下得到的,若考虑初始缺陷(如初始应力、初始偏心、初始弯 为理想线弹性条件下得到的,若考虑初始缺陷(如初始应力、初始偏心、初始弯
曲、残余应力等),直接引用《钢结构设计规范》中b类曲线来设计L形钢柱即可。
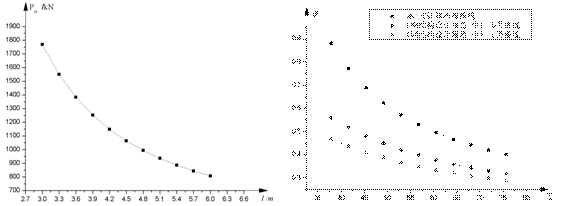
图3 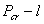 曲线 图4 曲线 图4 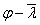 曲线 曲线
4、总结
本文提出了L形钢异型柱,并用弹性薄壁柱理论的任意截面开口薄壁柱弯扭屈曲相关方程,为L形截面钢柱应用研究提供了理论基础。本文提出的L形截面钢柱由普通热轧H型钢和T型钢组合而成,不仅满足了钢结构住宅建筑的需要,而且它不同于角钢而具有边缘约束构件,故承载力比同截面面积的H型钢高,有进一步研究的理论和实际意义。限于篇幅,L形柱压弯承载力应用研究将另文发表。
参考文献
[1]. 陈骥,钢结构稳定理论与设计,科学出版社.2001
[2]. 中华人民共和国国家标准,《钢结构设计规范》GB50017-2003
|