|
当轴心受压时,有 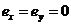 ,再将方程(2)两边同时除以 ,再将方程(2)两边同时除以 ,展开后则方程(2)成为 ,展开后则方程(2)成为

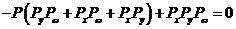 (3) (3)
这就是L形钢异型柱在轴心受压情况下的稳定方程,它是关于压力P的一元三次方程。我们将根据一元三次方程根的性质,求解它的根。
2 换算长细比
由文献[1]我们知道,方程(3)是齐次方程(4)的特征方程。
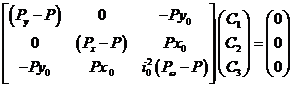 (4) (4)
将方程(4)写成如下形式:
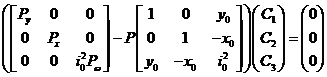
令:  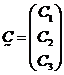
得: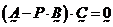 (5) (5)
因为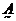 为对角阵,且各主元素都大于零,而 为对角阵,且各主元素都大于零,而 ,所以矩阵 ,所以矩阵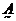 、 、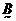 的各阶顺序主子式的行列式均大于零,且矩阵 的各阶顺序主子式的行列式均大于零,且矩阵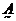 、 、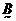 均为实对称矩阵,根据线性代数有关定理可知 均为实对称矩阵,根据线性代数有关定理可知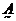 、 、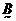 均为正定矩阵,L形钢异形柱轴心受压承载力是正定系统。类比机械振动理论 均为正定矩阵,L形钢异形柱轴心受压承载力是正定系统。类比机械振动理论 问题,其中 问题,其中 为系统的刚度矩阵, 为系统的刚度矩阵,  为系统的质量矩阵, 为系统的质量矩阵, 、 、 都为正定矩阵,则由 都为正定矩阵,则由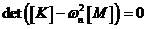 解出的 解出的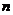 个 个 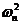 的值,即 的值,即 、 、 矩阵对的广义特征值均为正实数,且互不相等。由此得出,本文方程 矩阵对的广义特征值均为正实数,且互不相等。由此得出,本文方程  的根是 的根是 、 、 矩阵对的广义特征值 矩阵对的广义特征值 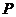 ,展开后一元三次方程(3)的根是三个正的互不相等的实数。求解如下。 ,展开后一元三次方程(3)的根是三个正的互不相等的实数。求解如下。
令:  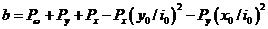
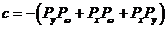  (6) (6)
于是方程(3)就可以简写为:
 (7) (7)
再令  ,方程(7)就可以表示为: ,方程(7)就可以表示为:
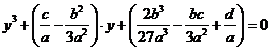 (8) (8)
令: 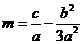 
所以,方程(8)就可以表示为: 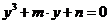 (9) (9)
根据本文所研究的问题,可以证明
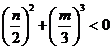 (10) (10)
  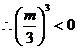 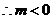 (11) (11)
由此,我们利用卡丹公式的根的三角函数表达形式,就可以得出一元三次方程(9)的三个根 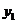 、 、  、 、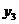 为: 为:
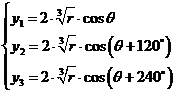
(12)
式中: 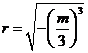  (13) (13)
所以,一元三次方程(3)的三个根 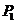 、 、 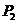 、 、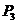 为: 为:
  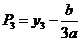 (14) (14)
由于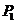 、 、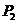 、 、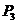 为三个互不相等的正实根,因此,L形钢异形柱在轴心受压情况下的临界力的理论解为: 为三个互不相等的正实根,因此,L形钢异形柱在轴心受压情况下的临界力的理论解为: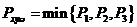 。下面比较 。下面比较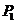 、 、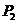 、 、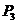 三个力的大小: 三个力的大小:
通过分析可知: 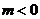 , ,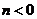  , , 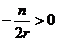
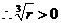 , ,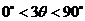 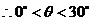 , ,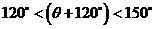 , ,
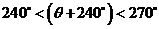
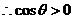 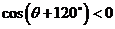 、 、 且 且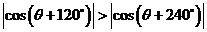
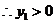 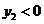  且 且 又 又 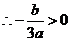
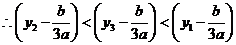 即 即 
即L形钢异形柱在轴心受压情况下的稳定临界力的理论解为:
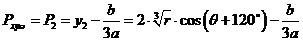 (15) (15)
若定义: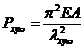 (16) (16)
式中  为柱换算长细比,结合(15)式,并将(6)、(13)等参数代入,再 令 为柱换算长细比,结合(15)式,并将(6)、(13)等参数代入,再 令


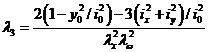

 (17) (17)
则得: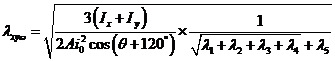 (18) (18)
这就是L形截面柱换算长细比。
上一页 [1] [2] [3] 下一页
|