|
1 轴心受压实用计算公式
实际上,轴心受压柱的受力性能受许多因素影响,主要的因素有截面中的残余应力、杆轴的初弯曲、荷载作用点的初偏心以及杆端的约束条件等。这些因素的影响是错综复杂的,其中残余应力、初弯曲和初偏心都是不利的因素,并被看作是轴心压杆的缺陷,而实际结构中的受压杆件大都是存在着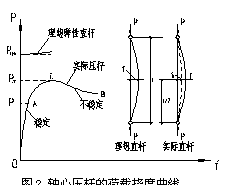 上述缺陷的,因此使得柱的轴向压力往往达不到理论值 上述缺陷的,因此使得柱的轴向压力往往达不到理论值 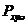 ,而是如图2所示的OAB曲线形成极值型弯曲破坏[2],最大值为 ,而是如图2所示的OAB曲线形成极值型弯曲破坏[2],最大值为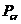 。缺陷对于短柱影响较小可忽略不计, 。缺陷对于短柱影响较小可忽略不计,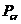 可达到 可达到 ,但对较长柱 ,但对较长柱 ,属于弯曲强度问题。 钢结构理论中柱的缺陷性分析引入稳定系数 ,属于弯曲强度问题。 钢结构理论中柱的缺陷性分析引入稳定系数 ,与柱长细比 ,与柱长细比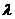 制成表格供查取。系数 制成表格供查取。系数 综合考虑了各种缺陷影响,得 综合考虑了各种缺陷影响,得 。本文将直接引用钢结构理论中柱缺陷分析结果[3],由换算长细比 。本文将直接引用钢结构理论中柱缺陷分析结果[3],由换算长细比 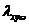 查b类截面稳定系数 查b类截面稳定系数 ,就得到实际的L形截面钢柱轴心受压的实用计算公式 ,就得到实际的L形截面钢柱轴心受压的实用计算公式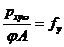 (19) (19)
设计用: 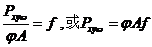 (20) (20)
我们将L形截面钢柱弯扭屈曲用换算长细比的方法换算为弯曲屈曲,虽然换算是按弹性进行的(方程(3)的解),但由于弯曲屈曲的  值非弹性和初始缺陷,这就相当于L形截面钢柱弯扭屈曲间接考虑了非弹性和初始缺陷,公式(19)或(20)就是我们的L形截面钢柱轴心受压弯扭屈曲的实用设计计算公式。我们定义的L形截面有翼缘存在,比轧制等边角钢截面抗扭能力强,可将其归于b类截面,我们还将用试验验证。 值非弹性和初始缺陷,这就相当于L形截面钢柱弯扭屈曲间接考虑了非弹性和初始缺陷,公式(19)或(20)就是我们的L形截面钢柱轴心受压弯扭屈曲的实用设计计算公式。我们定义的L形截面有翼缘存在,比轧制等边角钢截面抗扭能力强,可将其归于b类截面,我们还将用试验验证。
为了便于计算换算长细比 ,我们以H型钢组合成如图1所示的多种L形截面作为常用,计算给出了截面几何性质如 ,我们以H型钢组合成如图1所示的多种L形截面作为常用,计算给出了截面几何性质如 、 、 、 、 、 、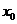 、 、 、 、 、 、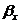 等成表,限于篇幅,这里不再列出。 等成表,限于篇幅,这里不再列出。
4 试验
取图3所示截面尺寸,制作了3组试件,长度分别为1.0m、2.0m和3.0m,每组两根。为确保加载到轴心,在柱端板上的柱截面形心处放置小垫块,荷载加在该垫块上。试验装置见图4所示。在柱中 部翼缘上贴有应变片和安装了位移计,通过计算机随时记录应变和变形数值。试验之前先做了柱材性试验,实测出 部翼缘上贴有应变片和安装了位移计,通过计算机随时记录应变和变形数值。试验之前先做了柱材性试验,实测出  以便有关计算引用。试验结果长柱有弯扭屈曲现象发生,短柱(1.0m)以弯曲屈曲为主,并有局部屈曲发生。三种长度柱的变形见图5、6、7所示,计算与试验结果对比见表1。P-λ曲线见图8所示。试验表明,试验值比计算值大,本文提出的实用计算公式(20)是合理的。 以便有关计算引用。试验结果长柱有弯扭屈曲现象发生,短柱(1.0m)以弯曲屈曲为主,并有局部屈曲发生。三种长度柱的变形见图5、6、7所示,计算与试验结果对比见表1。P-λ曲线见图8所示。试验表明,试验值比计算值大,本文提出的实用计算公式(20)是合理的。
表1 计算与试验对比
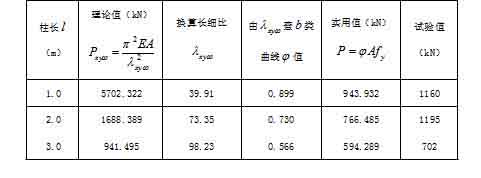
注:柱试件Q235B钢材,材性试验 256MPa 256MPa

结论
本文研究的L形截面钢柱由普通热轧H型钢和T型钢组合而成,不仅满足了钢结构住宅角柱在室内不暴露的建筑需要,而且它不同于角钢而具有边缘构件,抗扭性能较好。用本文给出的换算长细比查规范b类截面的稳定系数 按公式(20)进行轴心受压计算可用于实际工程设计。本文的工作还为L形截面柱弯扭屈曲一般性方程化简奠定了基础。 按公式(20)进行轴心受压计算可用于实际工程设计。本文的工作还为L形截面柱弯扭屈曲一般性方程化简奠定了基础。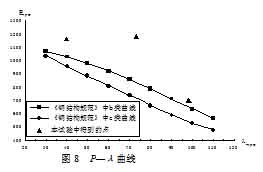
参考文献
[1]. 王明贵,张莉若,谭世友,钢异形柱弯扭相关屈曲研究,《钢结构》Vol. 21,No.87, 2006.
[2] 陈绍蕃主编,高等学校试用教材《钢结构》
,1986年3月.
[3]. 中华人民共和国国家标准,《钢结构设计规范》GB50017-2003
上一页 [1] [2] [3]
|